
(续)第十一篇 教学相长 学在教中 — 我的教学心得与感悟
我们用有趣的故事来说明无限范畴中整体与部份的一一对应。这就是所谓的希尔伯特(Hilbert)大酒店:希尔伯特先生开设了这样一个特殊的酒店,我们称它为《希尔伯特大酒店》:这个酒店有无穷多个房间,自数数是这些房间的号码。
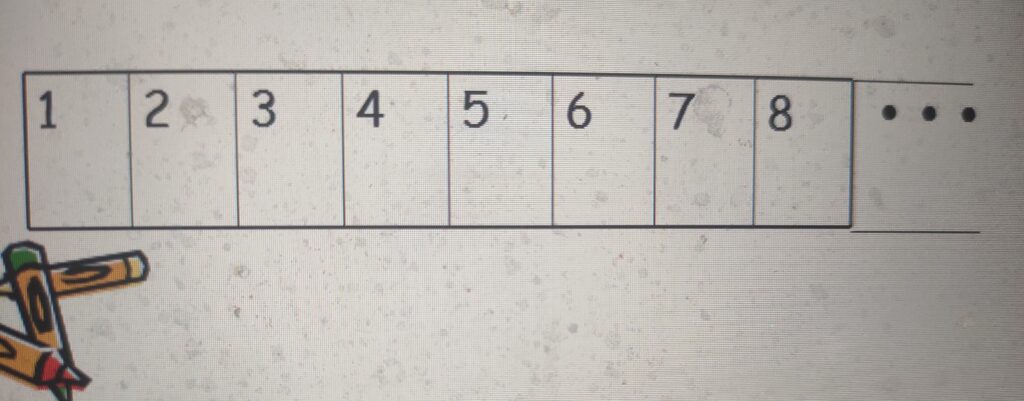
第一天,来了一个有自然数那么多人的代表团,一人一间,《希尔伯特大酒店》住满了。第二天,又来了一个旅客要求入住,并且也要一人一间。怎么办呢?酒店经理想到了如下办法得以解决:让住1号房间的客人住到2号房间去,住2号房间的客人到3号房间去,…,住n号房间的客人住到n+1号房间里去,…。这样,1号房间空出来了供新到的客人住。
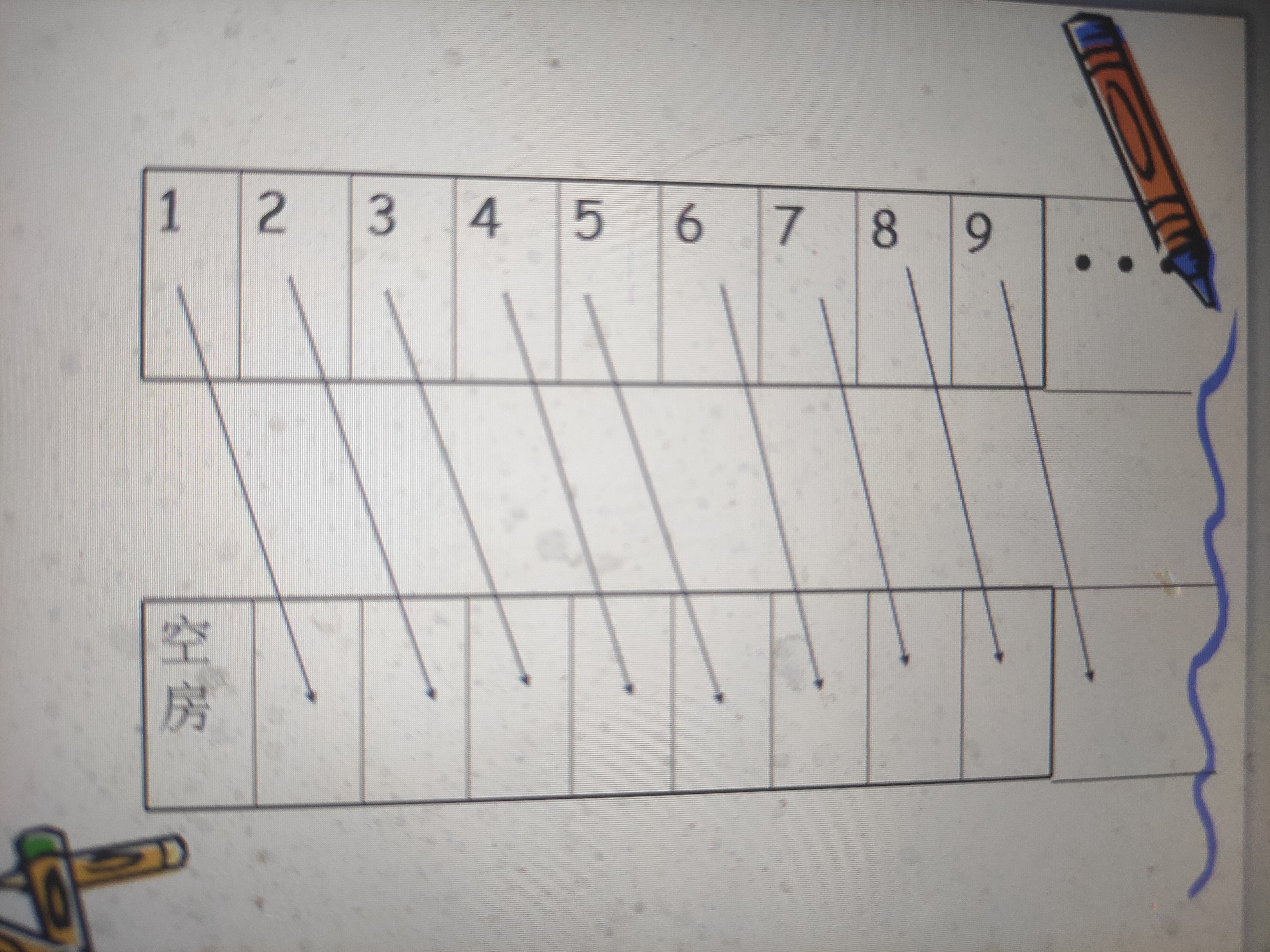
第三天,又来了一个有自然数那么多人的代表团.,也要求一人一间入住《希尔伯特大酒店》,这时,酒店经理没辙了,便去请教希尔伯特先生的女儿。希尔伯特先生的女儿给他想了个方法,经理照此办理,又把这个有自然数那么多人的代表团一人一间的安排进了酒店。希尔伯特先生的女儿给经理的办法是:让原来住在1号房间的客人住到2号房间去,住在2号房间的客人住到4号房间去,住在3号房间的客人住到6号房间去,…,以此类推,住在n号房间的客人住到2n号房间去,…。这样,原先的客人都住到2,4,6,…,2n,…等偶数号房间去了,而1,3,5,…,2n+1,…等奇数号房间正好供新到的有自然数那么多人的代表团一人一间住入《希尔伯特大酒店》。

第四天,来的客人更多了:是来了自然数那么多个代表团,而每个代表团都有自然数那么多客人,也要求一人一间入住《希尔伯特大酒店》。经理赶忙去找希尔伯特先生的女儿想办法,但希尔伯特先生的女儿也没辙了,只好去求教希尔伯特先生。希尔伯特先生给经理列了如下的一张表,让他按表中所列顺序的方法一个一个地把全部客人一人一间的按排住进《希尔伯特大酒店》:
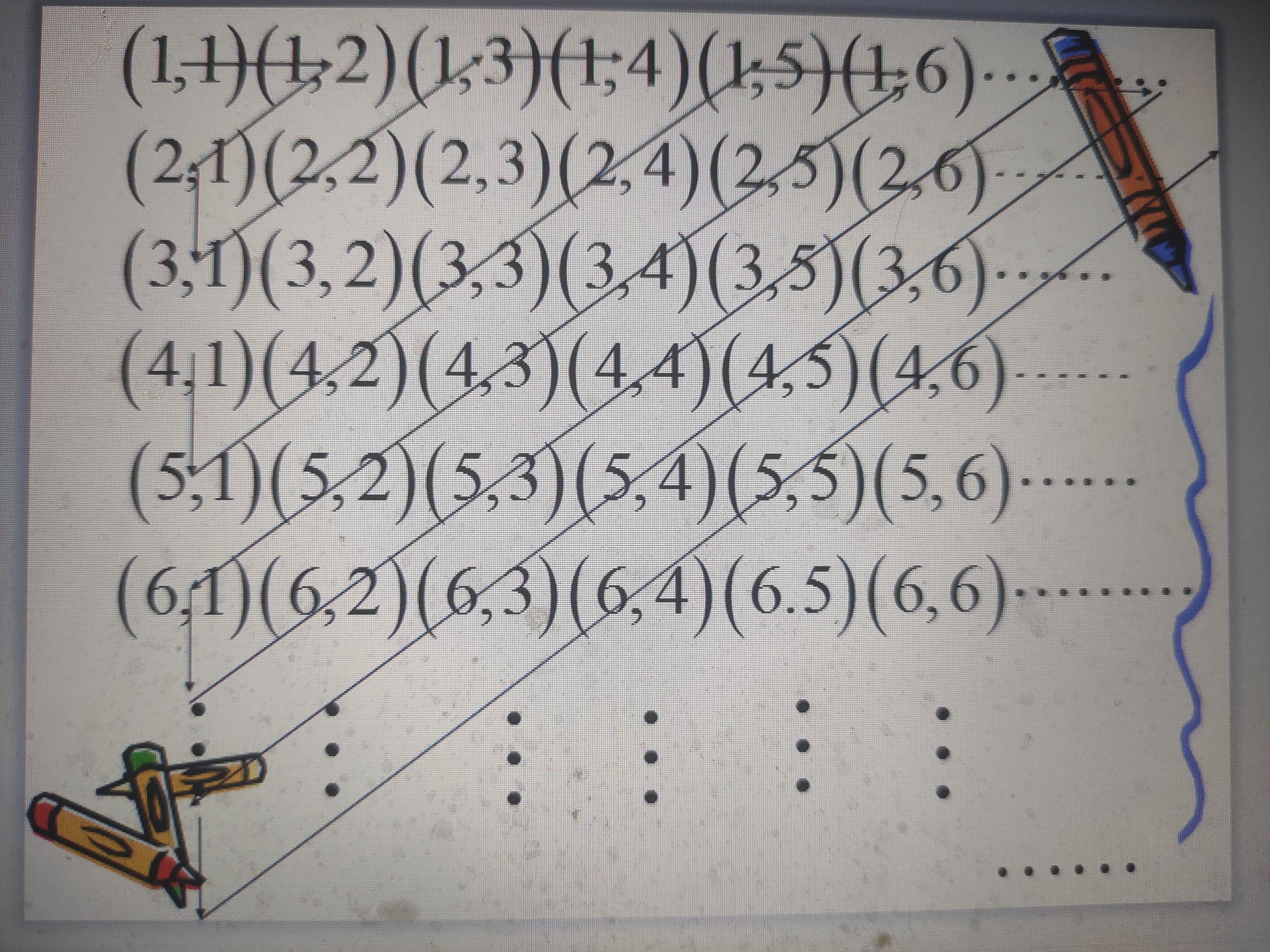
这个表中每一个坐标表示这“自然数那么多个代表团,而每个代表团都有自然数那么多客人”中的一位客人,并且这些团的全部客人都在这个表中有他的位置。这个表是向右向下无限扩展的,表的第一行表示序号为一的那个代表代表团中的每一位客人,比如(1, 1)表示这个代表团中序号为1的客人,以此类推。那根折线把这个表中的所有坐标都串上去了,这样所有的客人在折线上都有序了,可依这个序把他们一人一间的安排到希尔伯特酒店入住,实现了所有客人的要求。
这实际上是希尔伯特先生在100多年前所讲述的一个故事。希尔伯特先生是上一个世纪最伟大的数学家,他在上一世纪初的1900年8月6日召开的第二次国际数学家大会上所作的演说中所提出的《二十三个数学问题》是数学发展史上的一个重要里程碑,对20世纪的数学发展起了巨大的推动作用。希尔伯特先生的这个故事,就是为了说明无穷范畴中整体与部份的重要性质的。
这个故事说明了什么呢?它说明了正偶数集、自然数集与正有理数集这三个无穷集合的一个重要性质:这三个集合中,正偶数集是自然数系的子集,而自然数集是正有理数集的子集,但这三个集合的元素的个数是相等的。这恰好说明了,在无限范畴内,部份与整体的元素数目是可以相等的。
进一步的讨论可以确定:自然数集与有理数集,仅管自然数集是有理数集的子集,但二者中的数是一样多的,即:自然数与有理数是一样多的,有多少个自然数,就有多少个有理数。 这再一次说明,在无限范畴内,部份与整体在数量上是可以相等的。
上边这些内容,说到了一个自然科学的哲学思辨基础问题,哲学是自然科学的基础和出发点,我们现在所说的物理学,在相当长的历史时期内,是被称为自然哲学的,牛顿的巨著《自然哲学的数学基础》,讲的就是物理学中牛顿力学的微积分数学基础,在牛顿那个时代物理学就是被称为自然哲学的。而要追溯起自然科学的哲学基础,那就得从科学技术历史中古希腊一批先哲们对自然世界的讨论说起,而其中最有代表性的是古希腊的哲学家亚里士多德,以及他的老师柏拉图和柏拉图的老师苏格拉底。
我们再来看一些有趣的科学技术发展历程中的故事。说到概率论,大家一定会认为这门应用性极为广这的数学分枝应该产生在一个重要的历史背景中,但深究起来却有些荒唐和好笑,用今天“正能量”的话来说,它似乎有点持身不正出生不好,概率论其实是发源于关于赌博的事端中。公元1494年,一名意大利教师帕奇欧里出版了一本关于计算问题的教科书,提到了它他所遇到的一个赌金分配问题:两个赌徒约定一场赌博需要胜16局才算赢,当进行到甲胜15局,乙胜12局的时候,因故比赛中止,此时甲乙二人应如何分配赌金才合理。半个世纪之后,意大利数学家卡当对这个问题进行了更深入的讨论。又过了一百年,数学家巴斯卡受赌徒梅累所请,再次研究了这种赌金分配问题。后来,费尔马与惠更斯也参加了讨论,惠更斯更于1657年出版了一本叫《论赌博中的计算》的专著,这本书至今被公认为是概率论的第一部著述。
帕奇欧里是这样分配赌金的:因为甲己胜了15局,乙也胜了12局,因此应按15:12=5:4
的比例分配赌金,即甲得赌金的5/9,乙得赌金的4/9。多数的人对这一分配方法难以理解与接受,认为这种分配原则不够公平合理。 卡当提出的赌金分配方法是按照(1+2+3+4):1=10:1的比例分配赌金。他认为,不应从已完成的比赛结果来决定赌金分配,而应由剩下的比赛次数来决定赌金分配。这个思维是概率思想的极好开端,但人们至今也不明白,卡当是如何考虑到这种10:1的分配比例的。赌徒梅累提出并由巴斯卡、费尔马、惠更斯等数学家肯定的赌金分配方法是15:1,即甲分得赌金的15/16,乙分得赌金的1/16。在《论赌博中的计算》一书中,对这种赌金分配方法的思想进行了深入地讨论。这种讨论对概率论的发展起到了十分积极的推动作用。
海王星被称笔尖下发现的行星,当年天文学家用牛顿万有引力定律已经成功预测了“金木水火土”在宇宙中的正确位置,可是用同样的方法来计算天王星的位置,却老是和观测结果稍有不符,天王星的运行轨道不准确。符合逻辑的结论是,在天王星以外,可能有一颗未知的行星对天王星施加着他们没有考虑到的引力吸引。英国剑桥大学一位27岁的数学系学生亚当斯开始利用课余时间解决这个问题。 1845年9月, 他终于计算出了那颗未知行星应有的位置,如果那颗行星那样运行的话,就能说明天王星轨道不准确的原因。可是,他把他的计算资料送到了英国天文台后,他的努力并未引起当时英国天文学家们的兴趣。在同一时期,另有一位法国的年轻天文学家勒威耶也在独立地研究这个问题,他在亚当斯之后半年完成研究工作,得出了与亚当斯相同的结果。勒威耶非常幸运,他找到德国天文学家伽勒帮助检查他所指出的那片天区是否有一颗未知的行星。伽勒于1846年9月23日夜晚开始搜寻,他和他的助手迪阿雷斯特仅用了一个小时就找到了一颗星象图上没有标记的八等星。当这一结果向全世界发布后,英国天文学家才想到了亚当斯的材料。谦虚的勒威耶就要把第一个发现海王星的功劳给亚当斯,但亚当斯也不接受,认为第一个找到海王星的应该是勒威耶。后来人们认为海王星是他们两个找到的。
(未完待续)
许仁忠:路漫漫,吾将上下求索: 我生活中的繁琐小事(295)
许仁忠:路漫漫,吾将上下求索: 我生活中的繁琐小事(294)
许仁忠:路漫漫,吾将上下求索: 我生活中的繁琐小事(293)
许仁忠:路漫漫,吾将上下求索: 我生活中的繁琐小事(292)
许仁忠:路漫漫,吾将上下求索: 我生活中的繁琐小事(291)
许仁忠:路漫漫,吾将上下求索: 我生活中的繁琐小事(290)
许仁忠:路漫漫,吾将上下求索: 我生活中的繁琐小事(289)
许仁忠:路漫漫,吾将上下求索: 我的人生回忆 (26)
许仁忠:路漫漫,吾将上下求索: 我的人生回忆 (94)
许仁忠:路漫漫,吾将上下求索: 我的人生回忆 (45)
许仁忠:路漫漫,吾将上下求索: 我生活中的繁琐小事(288)
许仁忠:路漫漫,吾将上下求索: 我生活中的繁琐小事(287)
许仁忠:路漫漫,吾将上下求索: 我生活中的繁琐小事(286)
许仁忠:路漫漫,吾将上下求索: 我生活中的繁琐小事(285)
许仁忠:路漫漫,吾将上下求索: 我生活中的繁琐小事(284)
许仁忠:路漫漫,吾将上下求索: 我的“大学”(192)
许仁忠:路漫漫,吾将上下求索: 我生活中的繁琐小事(283)
许仁忠:路漫漫,吾将上下求索: 我生活中的繁琐小事(282)
许仁忠:路漫漫,吾将上下求索: 我生活中的繁琐小事(281)
许仁忠:路漫漫,吾将上下求索: 我生活中的繁琐小事(280)
许仁忠:路漫漫,吾将上下求索: 我的“大学”(175)
许仁忠:路漫漫,吾将上下求索: 我生活中的繁琐小事(279)
许仁忠:路漫漫,吾将上下求索: 我生活中的繁琐小事(278)
许仁忠:路漫漫,吾将上下求索: 我生活中的繁琐小事(277)
- 许仁忠:路漫漫,吾将上下求索: 我的人生回忆(前言) - 01/28/25
- 欧州旅游:中东欧(三) - 01/27/25
- 许仁忠:路漫漫,吾将上下求索: 我的“城南纪事”(202) - 01/26/25


