无穷之惑

无穷之惑
杨益民
2023/04/24

“我看见了它，但是我不相信它！”
――摘自康托尔1877年给戴德金的信

前面写了《芝诺悖论与庄子二分法》，那是一个由无穷引起的思考。无穷的概念对于人类的感官、常识和直觉一直都是一种挑战。这篇帖文将介绍一些数学中关于无穷的有趣例子，浏览无穷的概念是如何挑战人类的感官与直觉。

一、芝诺悖论与庄子二分法（见78621同名文章）

二、宇宙的尘埃——康托三分集

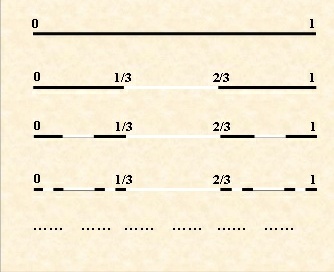
康托三分集构造步骤如下：

（1）将长度为1的线段三等分，删去中间的一段；
（2）把剩下的两段再各三等分，再删去它们中间的一段，
（3）重复（1）-（2）的步骤，如此无穷的继续做下去。

这样无穷次分割丢弃后剩下的点子的集合称为“康托三分集”。如图所示

我们的问题是：
（1）丢弃的部分的总长度是多少？
（2）余下的康托三分集的长度又是多少？
（3）康托三分集包含有多少个点？

丢弃部分的总长度L=1/3+2/3² +2²/3³ +……+2^n-1/3ⁿ +……

=1/3〔1+2/3+(2/3)² +……+(2/3)^n-1 +……〕=1/3〔1/（1-2/3）〕=1

因为这条线段未分割前长度为1，所以剩下部分的总长度（康托三分集的长度）=0。

而且显然剩下部分所包含的点子（康托集所包含的点子）有无穷多。这无穷多的点像“尘埃”似的散布在［0，1］区间上。所以，康托集被形象的称为“康托尘埃集”。

有趣且吃惊的是康托尔证明了：康托尘埃集所包含的点子数与［0，1］区间上的点子一样多。（这里我们不给出其证明，只陈述这一事实。）

把［0，1］区间挖的千疮百孔，丢弃部分的总长度与［0，1］区间一样长，而剩余的部分的长度为0，似乎把整个［0，1］区间全部丢弃了。但残余点的个数又与［0，1］区间上的点一样多，又似乎什么都没有丢。

这真是太奇怪，太违反直觉与常识了！

因此，康托尔大叫：“我看见了它，但是我不相信它！”

点是0维，线是1维，面是二维，体积是三维。那么这个奇怪的康托尔尘埃集是几维的呢？

事实上，康托集尘埃的维数介于0，1之间(具体数值是ln(2)/ln(3)=0.631)，分数维！邪乎吧！

三、科赫雪花曲线

1904年瑞典数学家科赫在其论文《从初等几何构造的一条没有切线的连续曲线》中构造出如下曲线――科赫雪花曲线。

这种曲线的作法是：
（1）从一个正三角形开始，把每条边分成三等份；
（2）以各边的中间长度为底边。分别向外作正三角形；
（3）把“底边”线段抹掉（这样就得到一个六角形，它共有12条边）；
（4）在每条边重复步骤（1）-（3）；
（5）反复无穷地这样进行下去，就会得到一个“雪花”样子的曲线。

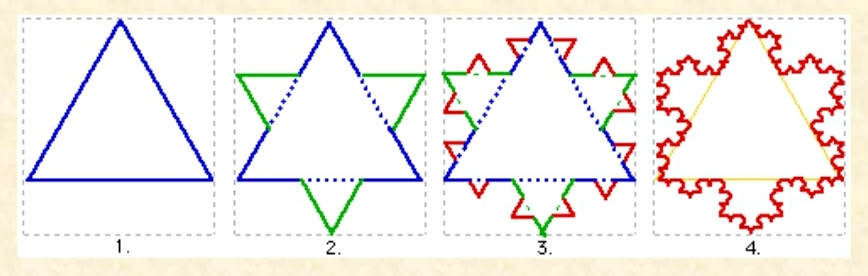
注：可网上搜索科赫雪花曲线的动态变化过程图。

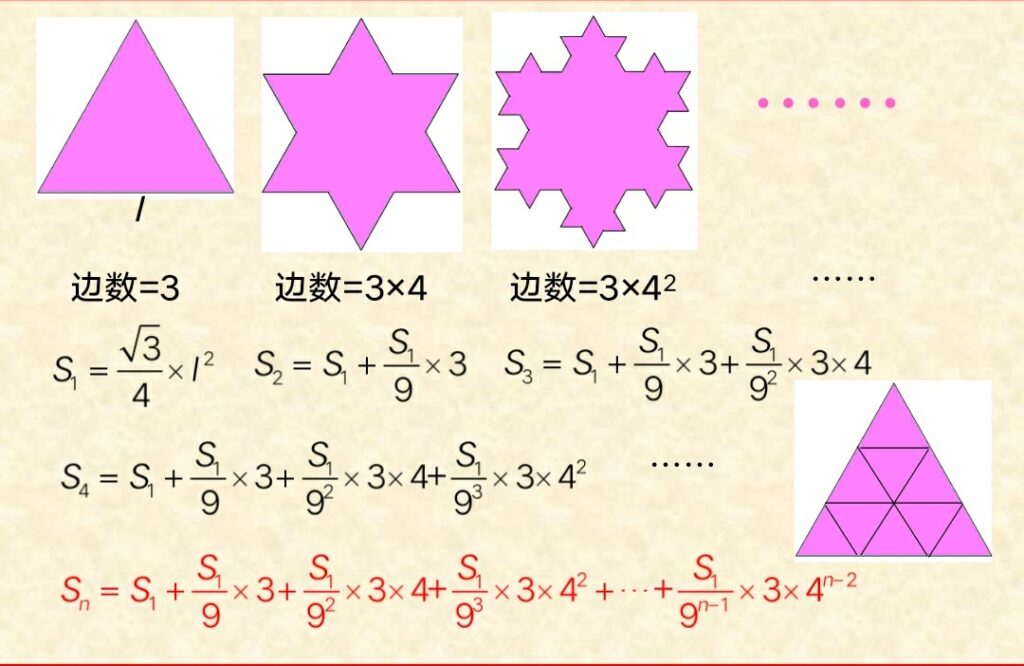
问题1：科赫雪花曲线的周长是多少呢？

L₁ =3l，L₂ =4/3×(3l），L₃ =(4/3)² ×(3l），……，

……，Ln=(4/3)^n-1×(3l），……

这是一个公比为4/3的等比数列：L₁ ，L₂ ，L₃ ，……，Ln，……，无限迭代下去，科赫雪花曲线的总周长为Ln的极限

Ln=(4/3)^n-1×(3l）――>∞（n――>∞）

即：每往下迭代作图一次，其周长均以公比4/3为因子增长，无限作下去其周长将趋于无穷大。

问题2：科赫雪花曲线所围闭的面积是多少呢？

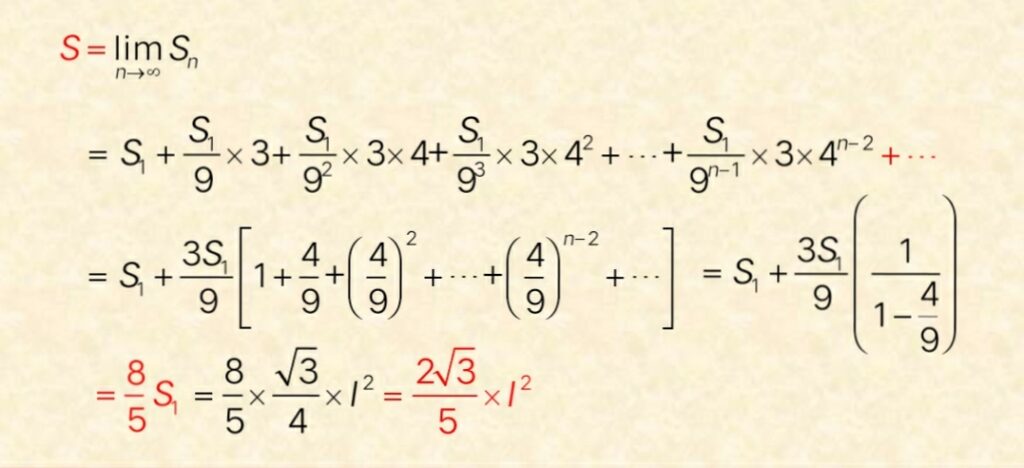
我们又看到一个有违我们直观感觉的奇怪现象：

（1）一块有限大的面积却有一条无穷大的边界！

（2）注意到了吗？科赫雪花曲线残留在初始三角形每条边上的点集就是康托尘埃集。

（3）不仅科赫雪花曲线的总长度无穷，而且曲线上任何两点之间的距离也是无穷大，不管这两点看起来有多么接近（因为在每个迭代阶段其长度都在以4/3的因子增长）。

四、谢尔宾斯基三角、地毯与海绵

谢尔宾斯基构造的著名谢尔宾斯基三角，如下图

谢尔宾斯基三角构造方法如下：
（1）取一个实心三角形（多数情况取等边三角形）；
（2）沿三角形的三边中点连线，将它分成4个小三角形；
（3）去掉中间的那一个小三角形；
（4）对其余3个小三角形重复上述过程（1）-（3）。

问题1：无限迭代地作下去，谢尔宾斯基三角形余下部分的面积是多少？

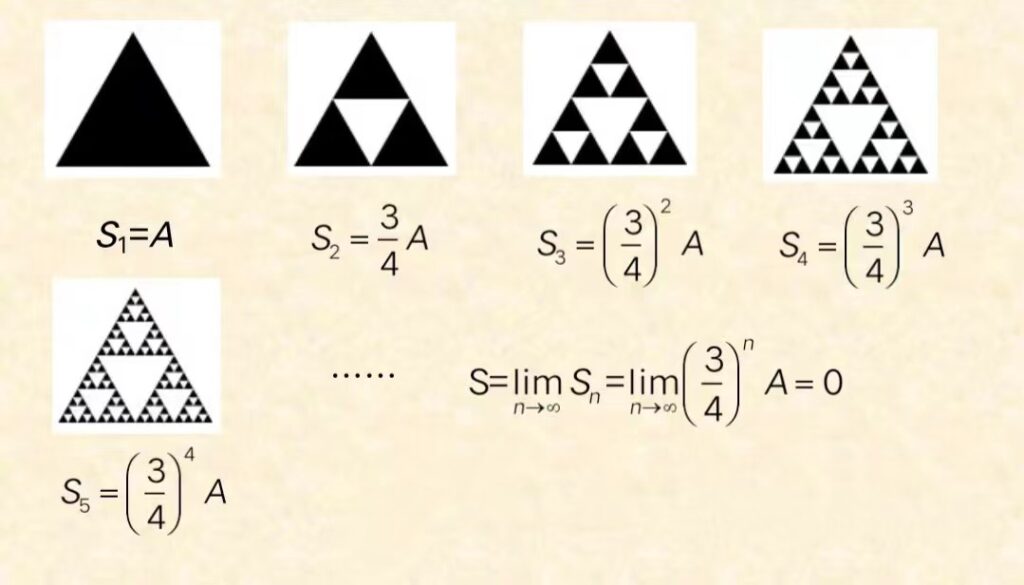
在一块三角形地块上祖祖辈辈挖呀挖，世世代代挖下去，挖得千疮百孔，万疮亿孔，……，可以想象其剩下的地块的面积趋于零，但永远永远也挖不完。

这是不是与“庄子二分法”有异曲同工之妙啊！

问题2：无限迭代地作下去，谢尔宾斯基三角形余下部分的周长是多少？

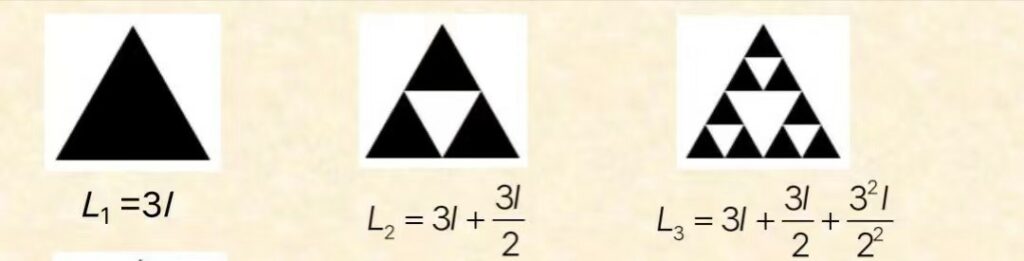
，……，L_n =3l +(3/2) l +(3/2)² l +……+(3/2)^n-1 l ，……

周长L=3l +(3/2) l +(3/2)² l +……+(3/2)^n-1 l +……=∞（从第二项起公比q=3/2>1）

谢尔宾斯基三角的面积趋于零，但它的周长却趋于无穷大。无穷长的周长围闭的面积却趋于零。岂不怪哉！

谢尔宾斯基地毯

谢尔宾斯基地毯与谢尔宾斯基三角类似，如果无限迭代地作下去，面积将逐渐消失趋于零，而地毯的周长却趋于无穷大。

门格―谢尔宾斯基海绵

（1）将正方体等分切割成27个小正方体（每个面9等分）；
（2）抽去体心与面心处的共7个小正方体；
（3）对剩下的20个小正方体重复（1）―（2）的步骤；
（4）无穷次如此迭代作下去……
将得到如下门格―谢尔宾斯基海绵

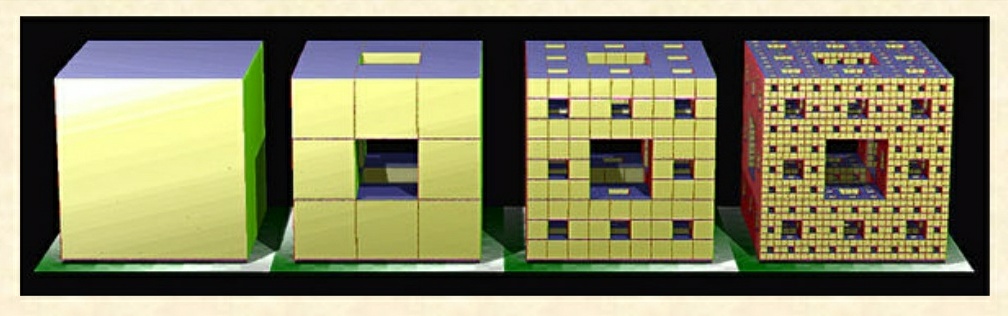
门格―谢尔宾斯基海绵是康托三分集与谢尔宾斯基地毯在三维空间的推广。 它首先由奥地利数学家卡尔―门格于1962年研究拓扑维数的概念时提出。

（1）门格―谢尔宾斯基海绵的每一个面都是谢尔宾斯基地毯；

（2）门格―谢尔宾斯基海绵与原立方体的任意一条对角线的交集都是康托三分集。

（3）门格―谢尔宾斯基海绵的体积将随着无限迭代逐渐消失趋于零，而它的表面积却将趋于无穷大。

更是奇哉怪哉！挑战人们的想象与直觉！

五、皮亚诺曲线（希尔伯特曲线）

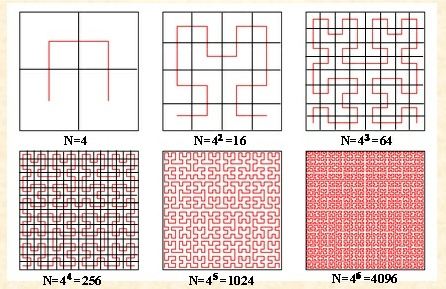
1890年，皮亚诺发现一种奇怪的连续参数曲线，当参数t在[0，1]区间取值时，曲线将遍历单位正方形中所有的点，得到一条充满正方形的曲线―皮亚诺曲线。稍后1891年希尔伯特在《数学年刊》上发表文章也发现了类似的曲线，并对此进行了较全面的研究。因此皮亚诺曲线也被称为希尔伯特曲线。

常识、经验与直觉都告诉我们：一维的东西不可能填满二维的方格。但皮亚诺曲线（希尔伯特曲线）恰恰给出了一个反例。

一条线是一维的，弯来弯去仍然是一维的。但皮亚诺曲线可以填满方格。难道皮亚诺曲线是二维的吗？或许我们应该重新思考“什么是维数”？或维数的定义应该修改或拓广。

面对无限，我们再次领会到人类的感官、常识与直觉是多么的无力！

芝诺悖论、康托三分集、科赫雪花曲线、谢尔宾斯基三角、地毯和海绵、皮亚诺曲线（希尔伯特曲线）哪一个图形不是对我们的感官、常识与直觉的巨大嘲弄，同时也是对传统维数理论的巨大挑战。它们还是美轮美奂的分形几何的最初源头之一。

从古希腊时代开始，只要涉及到无穷连最伟大的数学家、哲学家都感到熬头和心烦意乱。

下面让我们回到“最简单的”对数的认识的发展来看看无穷是如何挑战我们常人的感官、常识、直觉和心智的。

六、实数的连续性

自然数1，2，3，……有无穷多，每个自然数n都有一个后继n+1。所以，我们可以将自然数排序为：

1，2，3，……n，……

于是，我们知道它们中谁是“老几”，但不知道谁是“老幺”。不过我们知道谁紧挨着谁，而且每两个数之间的间隔始终为1。

为使加减法运算封闭（可行），我们将自然数集扩充到了整数集。

我们仍然可以将整数排序，知道它们中谁是“老几”，但不知谁是“老幺”。我们仍然知道它们谁挨着谁，而且每两个数之间的间隔始终为1。

下面是整数集的一种排序：

0，1，-1，2，-2，……，n，-n，……

为了使加减乘除运算都封闭（运算可行），我们又将整数集扩充到了有理数集。

问题1：你能将有理数排序吗？能指出它们中谁是老几吗？知道它们谁紧挨着谁吗？

你可能天经地义地认为：这哪有可能啊？！因为有理数无限稠密，即任何两个有理数之间总存在另一个有理数，从而任何两个有理数之间存在无穷多个有理数，也就是说有理数集合的元素之间不存在间隔！怎么可能排序呢？

伟大的数学家康托不愿意轻易接受这种直观的没有演绎严格证明的结论。他从“如何比较两个集合所含元素的多少”的角度来寻求突破。

比较两个集合所含元素的多少？容易啊！把两个集合所含的元素分别数一数，不就知道谁多谁少了吗？

可是有理数是无穷集，无穷集合怎么数啊？而且要数的话，总得知道谁是老大，谁是老二，……，谁是老n，……啊？有理数无限稠密你知道谁是“老大、老二、……”数得清吗？

康托的“幼儿园”新见解：――可在两个集合间建立一一对应来比较谁包含的元素多。

这就像老师问幼儿园的小朋友：咱们教室里小朋友多，还是凳子多啊？康托“小朋友”很聪明，他不数人数，也不数凳子，而是让全体小朋友都坐下。如果全坐下了，还有空凳子，那就是凳子多；如果凳子都坐满了，还有小朋友站着，那就是小朋友多。一个小朋友坐一个凳子，这就是小朋友与凳子一一对应。

例1 自然数集与偶数集之间可建立如下一一对应关系

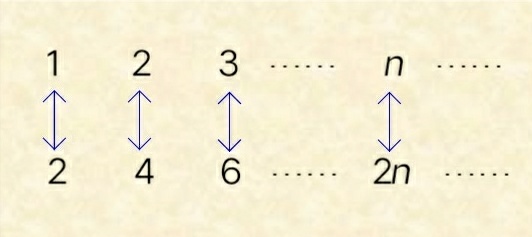
结论1：自然数与偶数一样多！类似的我们也可以得到自然数与奇数一样多。

例2 自然数集与平方数集之间的一一对应关系：

结论2：自然数与平方数也一样多。

全体大于部分，既是常识，也是欧几里得几何中不证自明的公理之一，甚至是我们的一种信仰。结论1、2太不可思议了！

下面看看康托如何将有理数排序，康托尔先把有理数集排列成如下的无穷阵列

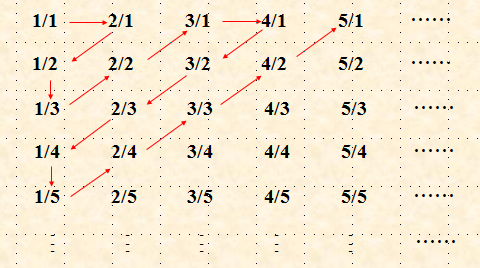
然后按箭头所指的顺序，对应自然数1，2，3，……，这样所有的有理数都与自然数一一对应了。

结论3：有理数集的元素间无限稠密不存在间隔，但它居然与元素之间很稀疏，存在很大间隔的自然数集、偶数集、奇数集、平方数集的元素一样多。

康托尔对此发现激动不已，大声惊呼“我看见了它，但我不相信！”

这些与自然数集的元素一样多的集合称为“可数无穷集”，简称“可数集”。

康托尔把一个集合所含元素的多少称为该集合的基数。显然，有限集合的基数就是它所含元素的个数。可数集的基数记为 ℵ ₀（读作阿列夫零）。

可以证明：
ℵ ₀ + ℵ ₀ + ……+ ℵ ₀ = ℵ ₀ （有限个可数集之和仍为可数集）
ℵ ₀ + ℵ ₀ + ……+ ℵ ₀ +……= ℵ ₀ （可数个可数集之和仍为可数集）

问题2：存在比可数集元素多的不可数集吗？

康托说：有啊！无理数集就是啊！

空口无凭，证明如下：

区间（0，1）中的实数包括：有理数（有限小数和无限循环小数）和无理数（无限不循环小数）。而有限小数总可以用无限循环小数来代替。例如0.5=0.4999……。所以（0，1）中的实数均可以表示为无限小数。

反设（0，1）中的实数是可数的，于是我们可以一个不漏地逐一列出（0，1）中的所有实数：

所以，区间（0，1）中的实数不可数，从而（0，1）中的无理数不可数。进而全体无理数不可数，全体实数也不可数。

结论4：有理数有无穷多但可以一个一个地数清楚，而无理数比有理数多得多，多得数都数不清。

由于全体实数可以用一条直线来表示，这就意味着：尽管有理数无限稠密的分布在实数直线上，但有理数留下的“无理数空洞”比“有理数非空洞”多得多。

这又是我们的直觉难以想象和接受的不可思异！

现在让我们回忆一下，√2不是有理数的演绎证明：

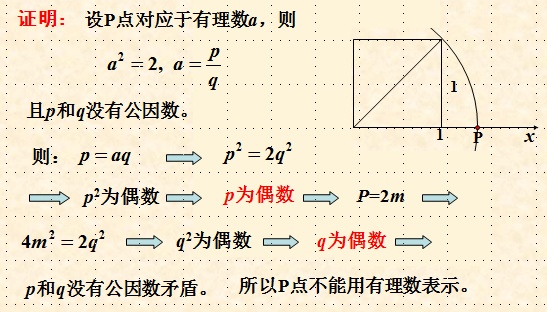
有理数的加减乘除仍为有理数，做任何实际的测量得到的数都只能是有理数，而且任何两个有理数之间都存在着有理数，所以直观上想有理数不仅是无限稠密，而且应该连续，即一条直线上布满有理数，别无它数。

毕达哥拉斯有理由天经地义地认为“万物皆数”，而且“数就是有理数”，即“万物皆为有理数”！

两直角边为1的正方形的斜边不是有理数，而且它还明明白白地摆在直线上（见证明中的P点）。

我的妈，那是个什么鬼啊！毕达哥拉斯解释不了，他的整个哲学的根基完全动摇了，岂能不惊恐？

如今康托尔还证明了那种“鬼”有无穷多，而且比有理数多得多！真是太反人类之感官与直觉了！毕达哥拉斯地下有知，还不从坟墓中蹦出来啊？！

后来康托尔们还证明了：

（1）实数与无理数一样多（基数相等），具有与实数相同的基数的集合称为连续集，其基数记为C。
（2）一条线段上的点与整个直线上的点一样多。
（3）存在无穷多基数大于C的无穷集。
（4）从任何无限集出发，通过构造其幂集，可以生成这个无限集的一个无穷谱系。例如2^ℵ ₀ =C。
……

每一个结论都是反直觉与常规的！

再举两个一一对应的例子，如下

将无穷远视为一个点，下图建立了圆与直线之间的一一对应关系。在这种观点下，圆与直线 ――“直”与“弯”这两个历来的对立面统一起来了。

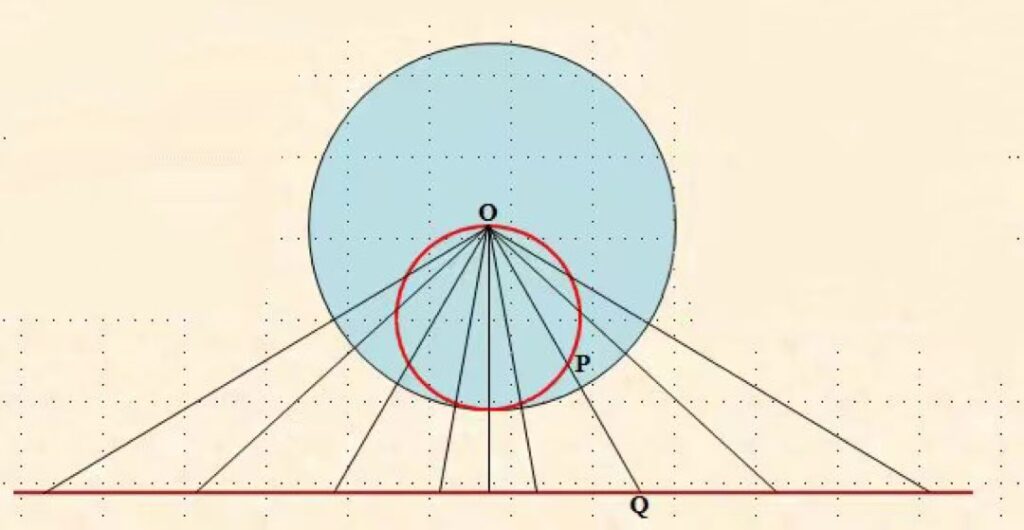
将这种方法推广到三维空间，我们得到球面与平面之间的一一对应关系。

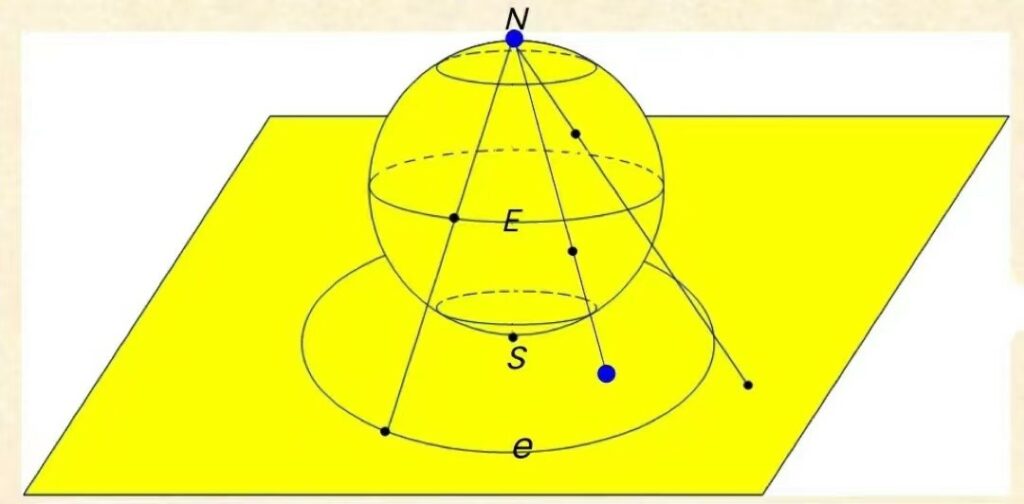
此一一对应的特征：纬度圈映射成围绕南极的同心圆，黄经圈（子午线）被映射成直线，地球上的赤道E变成地图上的圆e；整个北半球被影射到e外，整个南半球被映射到e内，北极点对应无穷远点。

问题3 存在基数小于C大于ℵ ₀ 的无穷集吗？即元素比全体自然数多，又比全体实数少的无穷集吗？

连续统假设：1874年康托尔猜测：在自然数集基数ℵ ₀ 和实数集基数（2^ℵ ₀ =C）之间不存在任何中间基数。

后来连续统假设又被推广为“广义连续统假设”。

1900年在第二届国际数学家大会上，希尔伯特发表了著名的历史演讲：揭开了20世纪数学历史发展的序幕。希尔伯特讲演的主要部分是23个未解决的数学问题，连续统假设被列为23问题的第一个。这些问题一直激发着数学家们的浓厚兴趣，在被誉为数学诺贝尔奖的菲尔兹奖的获奖者中，大多数的工作都与希尔伯特23问题有关。

希尔伯特（1862-1943）德国著名数学家，20世纪最伟大的数学家，被称为“数学界的亚力山大”。

19世纪末康托尔集合论的出现，使数学家们感到集合论可能成为整个数学大厦的坚强基石，因为所有的数学概念都可以归结为某种集合。数学可能会一劳永逸的摆脱“数学基础”的危机。

庞加莱在1900年第二次国际数学家大会上自信而兴奋地宣称：“”我们可以说，现在的数学已经达到了绝对的严格性！数学界一派乐观升平。

庞加莱（1854-1912）法国数学家、物理学家、科学哲学“批判学派”代表人物之一。

实际上，暴风雨正在酝酿，数学家们不知道他们将会被自己竖起的绞架吊死。1902年罗素提出了他的集合悖论，罗素悖论犹如晴天霹雳，震惊了整个数学界。第三次数学危机到了！

罗素（1872-1970）英国哲学家、数学家、逻辑学家，分析哲学的主要创始人，世界和平运动的倡导者和组织者。

德国数学家、数理逻辑的先驱弗雷格花了25年写就的《算数的基本法则》第二卷正要付印时，他收到了罗素的信。弗雷格在其著作的末尾加了一个附注：“一个科学家不可能遇到比这个更难堪的事情，即大厦将要竣工时，它的基础垮掉了。当这部著作将要付印时，罗素先生的信就使我处于这种境地。”戴德金也把将要付印的第三版《连续性及无理数》抽回来了。希尔伯特惊呼：“在数学这个号称可靠性和真理性的范例里，每个人所学、所教、所用的概念及结构和推理方法，竟然导出不合理的结果。如果数学思考也失灵的话，那么我们到哪里去找可靠性和真理呢？”